Notions de Mathématiques Appliquées à l'Informatique
Examen Fin Module 1 :
Exercice 1 : Questions de cours :* Donnez la définition d'un bit, d'un octet.
* Expliquez comment vous effectuez une conversion décimale - binaire.
* Expliquez comment vous effectuez une conversion binaire - décimale.
* Comment se termine en base 2 un nombre pair, et un nombre impair ?
* Quel est le nombre de symboles utilisés pour représenter un nombre dans une base B ? Donner un exemple.
Exercice 2 : Numération :
Effectuer les changements de base suivants :
1234(10) = ... (16)
138.145(10) = ... (2)
A9F(16) = ... (10)
3FE(16) = ... (4)
11001,01(2) = ... (16)
Effectuer les opérations suivantes :
0101011 + 0111011 = ...
1011 * 1010 = ...
10011 - 1001 = ...
111110111 / 101 = ...
7FE(16) - 3AB(16) = ...
4B9(16) + FFF(16) = ...
Exercice 3 : Algèbre de BOOLE & Tableaux de Karnaugh :
1. Réaliser les logigrammes des fonctions suivantes :

2. Peut-on simplifier le logigramme suivant qui utilise 4 portes OU Exclusives.

3. Simplifiez par Karnaugh la fonction suivante :

4. Optimisiez la fonction suivante à l’aide dela méthode de Quine Mc Cluskey.
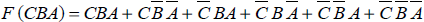
5. Établir les tables de vérité des fonctions suivantes, puis les écrire sous les deux formes canoniques (disjonctive et conjonctive)

Exercice 4 : Problème : l’additionneur complet
Pour effectuer une addition de deux nombres binaires de n bits, on additionne successivement les bits du même poids en tenant compte de la retenue de l’addition précédente comme le montre l’exemple suivant :

Il faut donc concevoir une cellule élémentaire appelée additionneur complet et qui permet de réaliser l’addition des bits ai et bi en plus de la retenue ci-1 de l’addition précédente, un tel additionneur est définit par le schéma suivant:
1- Dresser le tableau de vérité de l’additionneur complet
2- Simplifier les fonctions logiques Si et Ci
3- Dessiner le logigramme de Si et Ci

Notions de Mathématiques Appliquées à l'Informatique
Examen Fin Module 2 :
Exercice 1 :1) Remplir le tableau suivant en effectuant les conversions nécessaires.

2) développez l'équation si-dessous, puis simplifiez la au maximum (un tableau de Karnaugh peut aider) puis dessinez logigrammes réalisant cette fonction.

Exercice 2 : Etude se schéma :
1. Donner les équations de chaque sortie du schéma ci-dessous.

2. Ecrire la tabe de vérité des sorties A0, B0, C0, D0 et A1 en fonctions des entrées a, b, c et d.
Exercice 3 : Etude se schéma :
1. Établir les tables de vérité des fonctions suivantes, puis les écrire sous les deux formes canoniques (disjonctive et conjonctive) .

Exercice 4 : Etude se schéma :
1. Trois interrupteurs II, 12, et 13 commandent le démarrage de deux moteurs Ml et M2 selon les conditions suivantes :
- le moteur Mi ne doit démarrer que si au moins deux interrupteurs sont fermés (Ii= 1),
- dès qu'un ou plusieurs interrupteurs sont activés, le moteur M2 doit démarrer.
Réaliser un circuit logique permettant de réaliser Mi et M2 avec des opérateurs NON ET
2. Optimisiez la fonction suivante à l’aide de la méthode de Quine Mc Cluskey.

Autres EFM (s) sur le lien suivant :

ok
ReplyDelete